PPT for Chapter 2 - Probability and Distribution
Slide 2: Chapter Overview
Title: Overview of Probability and Distribution Content:
- Covers sample space, events, probability rules, conditional probability.
- Includes sensitivity/specificity, discrete distributions, binomial, uniform, and normal distributions.
- Explores mean, variance, and practical applications.
Slide 3: Sample Space (2.1)
Title: What is Sample Space? Content:
- Definition: Set of all possible outcomes of a random experiment (denoted as S).
- Examples:
- Rolling a die: S = {1, 2, 3, 4, 5, 6}
- Waiting time for a message: S = [0, ∞]
- Types:
- Finite (limited outcomes)
- Infinite (countable or uncountable)
Slide 4: Events (2.2)
Title: Understanding Events Content:
- Definition: Subset of sample space; specific outcome or set of outcomes.
- Example: Die roll event “even number” = {2, 4, 6}
- Types:
- Simple event: Single outcome (e.g., rolling a 3)
- Compound event: Multiple outcomes (e.g., even numbers)
- Operations: Union (\(A\cup B\)), Intersection (\(A\cap B\)), Complement (\(A^c\) or \(\bar{A}\))
Slide 5: Probability Basics (2.3)
Title: Probability: Measuring Likelihood Content:
- Definition: Likelihood of an event (0 = impossible, 1 = certain).
- Formula: For equally likely outcomes, P(A) = (Outcomes in A) / (Total outcomes in S)
- Example: Die roll, event “even number”: P(A) = 3/6 = 0.5
Slide 6: Basic Probability Rules (2.4)
Title: Key Probability Rules Content:
- Non-negativity: \(P(A) ≥ 0\)
- Normalization: \(P(S) = 1\)
- Addition Rule (Mutually Exclusive): \(P(A∪B) = P(A) + P(B)\)
- Complement Rule: \(P(A^c) = 1 - P(A)\)
Slide 7: Conditional Probability (2.5)
Title: Conditional Probability Content:
- Definition: Probability of event A given event B has occurred, P(A|B).
- Formula: \(P(A|B) = P(A∩B) / P(B)\)
- Example: Deck of 52 cards, \(P(Heart|Red) = (13/52)/(26/52) = 1/2\)
- Independence: \(P(A∩B) = P(A)·P(B)\) or \(P(A|B) = P(A)\)
Slide 8: Sensitivity and Specificity (2.6)
Title: Application: Sensitivity and Specificity Content:
- Context: Medical test accuracy.
- Sensitivity: P(Positive|Disease)
- Specificity: P(Negative|No Disease)
- Example: Test with sensitivity 0.95, specificity 0.90.
- 95% diseased test positive.
- 90% healthy test negative.
Slide 9: Discrete Distribution (2.7)
Title: Discrete Probability Distribution Content:
- Definition: Probability for discrete random variables (countable values).
- Probability Mass Function (PMF): P(X = x) for each value x.
- Property: Sum of probabilities = 1.
- Example: Daily complaints in a coffee shop (X: 0-3, Probabilities: 0.5, 0.3, 0.13, 0.07).
Slide 10: Mean and Variance of Random Variables (2.8)
Title: Mean and Variance Content:
- Mean (Expected Value): \(E(X) = \Sigma [x · P(X = x)]\), central tendency.
- Variance: \(Var(X) = \Sigma [(x - \mu)² · P(X = x)]\), measures spread.
- Standard Deviation: \(\sigma = \sqrt{Var(X)}\)
- Example (Die Roll): E(X) = 3.5, Var(X) ≈ 2.92, σ ≈ 1.71
Slide 11: Binomial Distribution (2.9)
Title: Binomial Distribution Content:
- Definition: Number of successes in n independent trials, success probability \(p\).
- Formula: \(P(X = k) = \frac{n!}{k!\cdot (n-k)!} · p^k · (1-p)^{n-k}\)
- Mean and Variance: \(E(X) = n·p, ~Var(X) = n·p·(1-p)\)
- Example: 10 coin flips (\(p=0.5\)), \(P(3~ \text{heads}) \approx 0.117\), \(P(6~ \text{heads}) \approx 0.205\)
Slide 12: Uniform Distribution (2.10)
Title: Uniform Distribution (Finite Interval) Content:
- Definition: Continuous variable equally likely between \(a\) and \(b\).
- Mean: \((a + b)/2\)
- Standard Deviation: \((b - a)/\sqrt{12}\)
- Example: Delivery time 20-40 mins, mean = 30 mins, P(25-30 mins) = 25%
Slide 13: Normal Distribution (2.11)
Title: Normal Distribution Content:
Definition: Bell-shaped, continuous, defined by mean (\(\mu\)) and standard deviation (SD: \(\sigma\)).
Empirical Rule:
- 68% within 1 SD
- 95% within 2 SDs
- 99.7% within 3 SDs
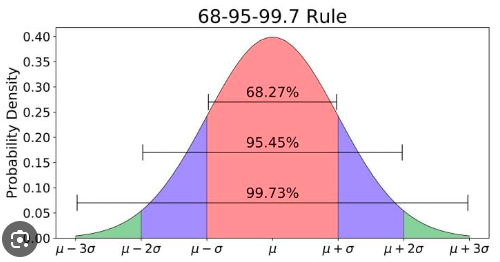
Example: IQ scores (\(\mu=100\), \(\sigma=15\)), \(P(85-115) \approx 68\%\)
Slide 14: Conclusion (2.12)
Title: Chapter Summary Content:
- Covered sample space, events, probability rules, conditional probability.
- Explored sensitivity/specificity in testing.
- Introduced distributions: discrete, binomial, uniform, normal.